笔者正在恶补数学……

1. 质数/素数
1. 欧几里得算法（Euclidean algorithm）
1. 费马小定理
1. 拓展欧几里得算法
- 4.1. 求逆元
1. 贝祖等式
1. 中国剩余定理
1. 一次一密（One-Time Pad）：
1. *分组密码
1. 线性反馈移位寄存器
1. RC4算法
- 10.1. 编程”实现”SHA-1: 只是demo
1. RSA与DSA算法
- 11.1. 编程“实现”RSA
1. Diffie-Hellman & Elgamal
1. 数字签名/证书
1. 椭圆曲线算法

数学基础

1. 质数/素数

只有1与本身两个因数的正整数。

6.3注：大整数分解困难问题是RSA算法的基础。另还有基于离散对数困难问题的Diffie-Hellman密钥交换协议、Elgamal加密以及DSA算法、基于椭圆曲线上离散对数困难问题的椭圆曲线密码体制。

整除的概念（拓展到多项式即为环）

素数的分布（黎曼猜想）、无限性证明（反证法）

Eratoshenes sieve

例：找出小于或等于30的所有素数。

步骤1：创建一个包含从2到30的所有整数的列表。

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

步骤2：从列表中选择第一个数，也就是2，将2的倍数从列表中移除。

2 3 5 7 9 11 13 15 17 19 21 23 25 27 29

步骤3：选择下一个未被标记的数，也就是3，将3的倍数从列表中移除。

2 3 5 7 11 13 17 19 23 25 29

步骤4：继续这个过程，选择下一个未被标记的数，直到达到了30的平方根（即5），因为在那之后的数都已经被标记或移除了。

步骤5：剩下的未被标记的数就是小于或等于30的所有素数。

E seive是确定性方法，而Miller Rabin素性检验是概率性方法。

2. 欧几里得算法（Euclidean algorithm）

我的理解中欧几里得算法即为，任意整数都可以被任意正整数线性表示，即a = q*b+r

欧几里得算法最大的应用是计算两个整数最大公约数（GCD）

例如，我们要计算 72 和 30 的最大公约数：
a = 72，b = 30。
72 除以 30 得到商 2 和余数 12。
12 不等于 0，所以将 30 的值赋给 a，将 12 的值赋给 b。
a = 30，b = 12。
30 除以 12 得到商 2 和余数 6。
6 不等于 0，所以将 12 的值赋给 a，将 6 的值赋给 b。
a = 12，b = 6。
12 除以 6 得到商 2 和余数 0。
余数为 0，所以最大公约数为 6。

而拓展欧几里得算法中GCD（a，b）也可以被a，b线性表示，即GCD（a，b）= sa + tb

欧拉函数与欧拉定理

https://zh.wikipedia.org/wiki/%E6%AC%A7%E6%8B%89%E5%87%BD%E6%95%B0

整数m＞1，（a，m）＝1，则a^E(m)与1同模m

3. 费马小定理

如果 p 是一个质数，a 是任意不可被 p 整除的整数，则有：

a^(p-1) ≡ 1 (mod p)

其中，^ 表示乘方运算，≡ 表示模运算的等价关系，即两边模 p 后的结果相等。

费马小定理的一个直接推论是，如果 p 是一个质数，a 是任意整数，则有：

a^p ≡ a (mod p)

但是反之，满足费马小定理的数不一定是素数。参见费马伪素数。

4. 拓展欧几里得算法

拓展欧几里得算法的基本思想是从最后一步欧几里得算法开始逆向推导，通过反复应用欧几里得算法的辗转相除过程，同时更新贝祖等式的系数。具体步骤如下：

初始化：令 a0 = a，b0 = b，x0 = 1，y0 = 0，x1 = 0，y1 = 1。
迭代计算：通过连续应用欧几里得算法的辗转相除过程，更新 a、b 和 x、y 的值，直到余数为 0。计算商和余数：q = a[i-1] // b[i-1]，r = a[i-1] % b[i-1]。
更新 a、b：a[i] = b[i-1]，b[i] = r。
更新 x、y：x[i] = x[i-2] - q * x[i-1]，y[i] = y[i-2] - q * y[i-1]。
输出结果：最大公约数为 b[n-1]，x[n-1] 和 y[n-1] 分别是贝祖等式 ax + by = gcd(a, b) 中的系数。

拓展欧几里得算法在密码学中常用于求解模逆元的问题，即找到一个数的乘法逆元（模某个数的余数下的倒数）。

4.1. 求逆元

5. 贝祖等式

对于任意两个整数 a 和 b，存在整数 x 和 y，使得它们满足以下等式：

ax + by = gcd(a, b)

其中，gcd(a, b) 表示 a 和 b 的最大公约数。

6. 中国剩余定理

中国剩余定理的一般形式如下：

给定一组正整数 m₁, m₂, …, mₙ 两两互质，以及任意的整数 a₁, a₂, …, aₙ，中国剩余定理说明存在一个整数 x，满足以下条件：

x ≡ a₁ (mod m₁)

x ≡ a₂ (mod m₂)

…

x ≡ aₙ (mod mₙ)

中国剩余定理可以找到一个满足多个模同余条件的整数。

以下为一个例子

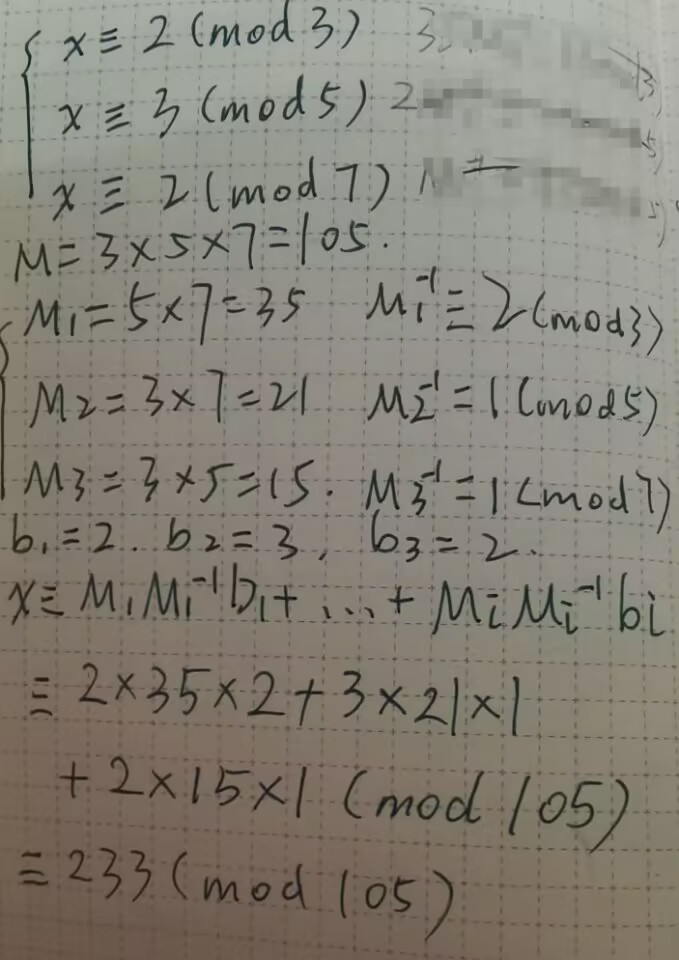
对称密钥加密

对称密钥加密是一种加密技术，其中使用相同的密钥（称为对称密钥）用于加密和解密数据。发送方使用密钥将明文（原始数据）转换为密文（加密后的数据），而接收方使用相同的密钥将密文转换回明文。

在对称密钥加密中，加密和解密过程使用相同的密钥，因此需要确保密钥的保密性。如果第三方获得了密钥，他们就可以轻松地解密和访问加密的数据。

7. 一次一密（One-Time Pad）：

一次一密是一种理论上具有绝对安全性的加密方法。它使用与明文长度相等的随机密钥进行异或运算，生成密文。密钥只使用一次，然后丢弃，因此称为一次一密。解密时，使用相同的密钥对密文进行异或运算，可以得到原始的明文。

OTP可以保证Perfect Secrecy。
联想：HTTPS 协议中的完美前向保密性（Perfect Forward Secrecy）是指在通信过程中，即使长期主密钥（long-term master key）被攻击者获得，之前的通信记录也无法被解密。在 HTTPS 中，完美前向保密性通过使用临时的会话密钥（session key），每次会话都生成一个新的临时密钥，用于加密通信。即使攻击者获取了主密钥，他们也无法通过该主密钥解密之前的通信记录，因为会话密钥已经发生了变化。

与PFS方法不同，OTP方法在实践中并不常用。

8. *分组密码

扩散与混淆
运行模式：*0+
OFB、CFB、CBC与ECB

Feistel密码结构

DES算法

明文密文分组长度64位，密钥64位（有效56位）

在 DES 的 ECB 模式中，如果在密文［1］分组中有一个错误，解密后仅相应的明文［2］分组受到影响然而在 CBC 模式中，将有错误传播。C1中的一个错误明显地将影响到 P1和P2的结果
(1)P2后的分组是否受到影响？
（2）设加密前的明文分组P1中有1比特的错误，问这一错误将在多少个密文分组中传播？
对接收者产生什么影响？

** DES的解密变换是加密变换的逆

DES算法中的轮结构与轮函数：16轮迭代轮函数共有8个s盒，其中每个i为6bit👉o为4bit。

*S盒如何将六位数据转换成4位：
例如，原始数据{1 0011 1 } ，取头尾数据11，十进制👉3即为行数

取中间数据0011，十进制👉3即为列数

在对应DES的S盒中查找就可以{十进制2👉0010 }

二/三重DES

AES算法

{此处需要群/域的基础}，见
https://zh.wikipedia.org/wiki/%E7%BE%A4 中的“定义”，https://zh.wikipedia.org/wiki/%E5%9F%9F_(%E6%95%B0%E5%AD%A6)

*AES算法的分组大小128位，三种密码标准：128、256、192（位）

**AES算法的过程：AddRoundKey👉SubstituteBytes👉ShiftRows👉MixColumns

SM4算法

分组长度128bit=密钥长度

流加密

9. 线性反馈移位寄存器

线性反馈移位寄存器（Linear Feedback Shift Register，简称LFSR）是一种在计算机科学和密码学中常用的序列发生器。它是由多个寄存器和一组反馈函数组成的，通过对寄存器中的位进行移位和异或操作来生成一个伪随机的二进制序列。

以下为一个例子：

10. RC4算法

哈希函数

引入哈希函数主要是为了保证数据完整性（这与隐私是不同的）

哈希函数是一种将输入数据（消息）转换为固定长度输出（哈希值）的函数。

抗原象性（Preimage Resistance）：对于给定的哈希值，很难找到一个与之对应的输入消息。也就是说，对于任意给定的哈希值，计算出其对应的输入消息应该是困难的。这意味着哈希函数应该是单向的，不可逆的。
抗第二原像性（Second Preimage Resistance）：给定一个输入消息，很难找到另一个不同的输入消息，使得它们具有相同的哈希值。也就是说，对于已知的输入消息，计算出与之具有相同哈希值的其他输入消息应该是困难的。
抗碰撞性（Collision Resistance）：很难找到两个不同的输入消息，使得它们具有相同的哈希值。也就是说，计算出两个具有相同哈希值的不同输入消息应该是困难的。
生日攻击（Birthday Attack）：生日攻击是一种特殊的攻击方式，利用生日悖论的原理，在较短的时间内找到两个具有相同哈希值的输入消息的概率较高。哈希函数应该抵抗生日攻击，即使在较长的时间内，找到具有相同哈希值的输入消息的概率也应该非常低。

生日攻击利用了概率学中的生日悖论，即在一组人中，只需要有23个人，就存在两个人生日相同的概率超过一半。类似地，在哈希函数中，由于输出空间的大小有限，当输入消息的数量足够大时，存在相同哈希值的输入消息的概率变得非常高。

为了抵抗生日攻击，通常的做法是使用更长的哈希值，例如SHA-256（256位哈希值）或SHA-3（Keccak）系列。这增加了哈希值的空间大小，降低了相同哈希值的概率。此外，还有一些专门设计的哈希函数，如HMAC（Hash-based Message Authentication Code）和SHA-3家族中的SHAKE函数，用于抵御生日攻击。

总结来说，即为产生MAC、传输MAC、验证MAC

10.1. 编程”实现”SHA-1: 见write-ups吧

如何利用哈希函数构造MAC？

*公钥密码

这部分需要详细学习（尤其是RSA非常重要）

对称密码体制缺乏开放的系统，依赖信道的可靠性、密钥管理困难，用户量增加时密钥空间急剧增大、难以实现抗抵赖。

公钥密码使用两个密钥：公开密钥与秘密密钥，加密解密非对称。模型：KeyGen()->(pk,sk);Enc(pk,m)->c;Dec(sk,c)->m

11. RSA与DSA算法

RSA证明方法：

安全性基于大整数分解：RSA的安全性基于大整数分解的困难性。证明方法是通过选择两个大素数 p 和 q，并计算它们的乘积 n = p * q。然后选择一个与 (p-1)(q-1) 互质的整数 e 作为公钥指数，以及计算出满足 (d * e) mod ((p-1)(q-1)) = 1 的私钥指数 d。公钥是 (n, e)，私钥是 (n, d)。

RSA的安全性取决于大整数分解的困难性，即从 n 中分解出 p 和 q 的困难性。大整数分解是一个耗时的计算问题，尚未发现有效的算法可以在可接受的时间内分解大素数的乘积。

11.1. 编程“实现”RSA

// 生成RSA密钥对
function generateRSAKeyPair() {
  var keySize = 2048; // 密钥大小
  var e = new BigInteger("65537"); // 公钥指数
  var p = BigInteger.probablePrime(keySize / 2, rng); // 随机生成素数 p
  var q = BigInteger.probablePrime(keySize / 2, rng); // 随机生成素数 q
  var n = p.multiply(q); // 计算 n = p * q
  var phi = p.subtract(1).multiply(q.subtract(1)); // 计算 φ(n) = (p - 1) * (q - 1)
  var d = e.modInverse(phi); // 计算私钥指数 d = e^(-1) mod φ(n)
  var publicKey = { e: e, n: n }; // 公钥 (e, n)
  var privateKey = { d: d, n: n }; // 私钥 (d, n)
  return { publicKey: publicKey, privateKey: privateKey };
}

// RSA加密
function rsaEncrypt(plaintext, publicKey) {
  var message = new BigInteger(plaintext); // 将明文转换为大整数
  var e = publicKey.e;
  var n = publicKey.n;
  var ciphertext = message.modPow(e, n); // 加密操作：c = m^e mod n
  return ciphertext.toString();
}

// RSA解密
function rsaDecrypt(ciphertext, privateKey) {
  var c = new BigInteger(ciphertext); // 将密文转换为大整数
  var d = privateKey.d;
  var n = privateKey.n;
  var plaintext = c.modPow(d, n); // 解密操作：m = c^d mod n
  return plaintext.toString();
}

// 示例用法
var plaintext = "Hello, RSA!";
var keyPair = generateRSAKeyPair();
var publicKey = keyPair.publicKey;
var privateKey = keyPair.privateKey;

var ciphertext = rsaEncrypt(plaintext, publicKey);
console.log("Ciphertext:", ciphertext);

var decryptedText = rsaDecrypt(ciphertext, privateKey);
console.log("Decrypted Text:", decryptedText);

DSA证明方法：

安全性基于离散对数问题：DSA的安全性基于离散对数问题的困难性。证明方法是通过选择一个大素数 p，并选择一个模 p 的生成元 g。然后生成一个私钥 x，满足 0 < x < p-1。计算公钥 y = g^x mod p。公钥是 (p, g, y)，私钥是 x。

DSA的安全性取决于离散对数问题的困难性，即计算 g^x mod p 中的 x 的困难性。离散对数问题是一个复杂的计算问题，在合理的时间内计算出离散对数是困难的。

12. Diffie-Hellman & Elgamal

Diffie-Hellman & Elgamal 也都基于数论中的离散对数问题

13. 数字签名/证书

消息认证（上文哈希）保护通信免受第三方攻击，但不能防止通信中另一方的欺骗和伪造

几个点：RSA/DSA数字签名算法、Elgamal数字签名体制、Schnorr签名体制

14. 椭圆曲线算法ECC

RSA、Elgamal为了保障安全性，常常采用长度很大的密钥，而椭圆密码体系可以用更小的尺寸得到同样的安全性。

总结公钥密码：公钥密码解决了对称密码“密钥管理麻烦、开放性差”的缺点，但这不意味著公钥密码的出现使对称密码“过时”了，也不意味着公钥密码体系更安全。同时，公钥密码加密解密速度较慢。

密钥管理与分配

最后说下这个，单钥加密体制（也就是对称加密体制）密钥分配的基本方法根据有无密钥分配中心KDC分为两种，密钥会话是有有效期的，其中面向连接协议在每次进行连接时都应更换密钥，而无连接协议可以在固定周期内使用固定密钥。

公钥加密体制的密钥管理涉及到密钥的分配、如何用“公钥体制”来分配对称密码体制所需的密钥。第一点不赘述。第二点有两种方法：简单分配（可能会被中间人攻击）、具有保密和认证的密钥分配（D-H协商、秘密分割、Shamir门限方案）

密码协议

数字承诺：Padersen数字承诺协议（也是基于离散对数问题）

不经意传输协议：A的秘密以0.5的概率传给B、协议执行完成后，B知道自己是否收到秘密，但A不知道B是否收到。

交互证明系统：零知识证明协议

Prev Home Next

⬆︎TOP

数论与密码学手册

目录